บทความนี้สปอยล์ซีรีส์เรื่อง Squid game ตอนที่ 7 บน Netflix (แต่เป็นการสปอยล์สิ่งที่ไม่สำคัญ มีผลต่อเนื้อเรื่องหลักน้อยมาก)

Squid game เป็นซีรีส์ลึกลับที่ให้คนมาเล่นเกมที่เดิมพันด้วยชีวิต ในเกมที่ 5 ตอนที่ 7 เกมที่ให้เล่นคือการข้ามสะพานกระจก

สะพานประกอบด้วยกระจก 36 บาน ในแต่ละก้าว ผู้เล่นจะต้องเลือกกระโดดไปยังกระจก 1 ใน 2 บานข้างหน้า

บานหนึ่งเป็นกระจกนิรภัยที่รับน้ำหนักได้ อีกบานเป็นกระจกธรรมดาที่จะแตกเมื่อกระโดดไป ทำให้ผู้เล่นตกลงมาตาย

ถ้าหากผู้เล่นคนใดสามารถข้ามสะพานทั้ง 18 ก้าวได้ก็จะผ่านเข้ารอบถัดไป โดยเกมนี้จะให้ผู้เล่น 16 คนเล่นตามลำดับด้วยสะพานเดิม

นั่นแปลว่าถ้าผู้เล่นก่อนหน้าเรากระโดดจากจุดเริ่มต้นไปยังกระจกก้าวที่ 1 เราก็จะรู้ทันทีว่าก้าวที่ 1 นั้นกระจกบานไหนปลอดภัย (ไม่ว่าผู้เล่นคนหน้าจะรอดหรือไม่)

เกมนี้ดูเหมือนผู้เล่นยิ่งคนหลังๆยิ่งมีโอกาสรอดมากขึ้น และถ้าลำดับที่เล่นมากกว่าจำนวนก้าว โอกาสรอดจะเป็น 100% ทันที (ถ้าไม่มีผู้เล่นคนใดจงใจแพ้หรือลืมผลของคนก่อนหน้า)

โอกาสรอดของการเล่นเกมนี้เป็นเท่าไหร่บ้างจะมาลองคำนวณกันในโพสต์นี้ (ในซีรีส์มีเนื้อหามากกว่านี้ แต่เราสนใจแค่นี้พอ)

ข้อสังเกตของเกมนี้มีอยู่ว่าผู้เล่นลำดับที่ n จะไม่มีทางตกบนกระจกก้าวที่ k เมื่อ k < n

ให้ deadExact(n,k) แทนความน่าจะเป็นที่ผู้เล่นคนที่ n ตกจากกระจกก้าวที่ k

และให้ survive(n,k) แทนความน่าจะเป็นที่ผู้เล่นคนที่ n จะรอดจากเกมที่มีความยาวสะพานเป็น k เราจะได้ว่า

และสำหรับกรณีมีผู้เล่นคนเดียว (หรือคนแรก) จะได้ว่า deadExact(1,k) = 0.5^k

จากนั้น สำหรับกรณีทั่วไปที่ผู้เล่นลำดับ n จะตกที่กระจกก้าวที่ k พอดีนั่นก็คือผลรวมของโอกาสที่

• ผู้เล่นคนที่ n-1 ตกที่กระจกก้าวที่ n-1 หลังจากนั้นผู้เล่นที่ n เดาถูกตลอดจนกระทั่งไปตกที่ก้าวที่ k
• ผู้เล่นคนที่ n-1 ตกที่กระจกก้าวที่ n หลังจากนั้นผู้เล่นที่ n เดาถูกตลอดจนกระทั่งไปตกที่ก้าวที่ k
• ผู้เล่นคนที่ n-1 ตกที่กระจกก้าวที่ n+1 หลังจากนั้นผู้เล่นที่ n เดาถูกตลอดจนกระทั่งไปตกที่ก้าวที่ k
• …
• ผู้เล่นคนที่ n-1 ตกที่กระจกก้าวที่ k-1 หลังจากนั้นผู้เล่นที่ n เดาผิดตั้งแต่ก้าวแรก

นำมาเขียนเป็นสมการได้ว่า

ลองเอามาเขียนเป็น golang ด้วยเทคนิค dynamic programming จะได้ประมาณนี้

package main

import (
	"log"
	"math"
)

var memoization = make(map[int]map[int]float64)

func deadExact(n, k int) float64 {
	if memoization[n] == nil {
		memoization[n] = make(map[int]float64)
	}
	if n > k {
		memoization[n][k] = 0
		return memoization[n][k]
	}
	if n == 1 {
		memoization[n][k] = math.Pow(0.5, float64(k))
		return memoization[n][k]
	}
	memoization[n][k] = 0
	for i := n - 1; i < k; i++ {
		memoization[n][k] += deadExact(n-1, i) * math.Pow(0.5, float64(k-i))
	}
	return memoization[n][k]
}

func survive(n, k int) float64 {
	deadProb := float64(0)
	for i := n; i <= k; i++ {
		deadProb += deadExact(n, i)
	}
	return 1 - deadProb
}

func main() {
	N := 16
	K := 18
	for j := 1; j <= K; j++ {
		log.Printf("Bridge: %d", j)
		for i := 1; i <= N; i++ {
			log.Printf("\tPlayer#%d survive chance: %.5f %%", i, survive(i, j)*100)
		}
	}
}

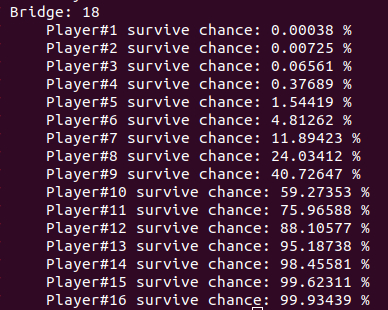โอกาสรอดของผู้เล่นแต่ละคนในซีรีส์

Interesting facts

• ถ้าลองคิด Expected value ว่าผู้เล่นหนึ่งคนจะเบิกทางให้คนหลังได้กี่ก้าว จะได้ออกมาที่ 2 ก้าว
• ถ้า k เป็นเลขคี่ ผู้เล่นลำดับที่ (k+1)/2 จะมีโอกาสรอด 50 %

Edited (25/09/2564 11:40): แก้โค้ดเป็น % และแปะผลลัพธ์สำหรับ scenario ในซีรีส์